Пребывание математического метода
вне математики (автор Александр Борисович Шур, кандидат технических наук, доцент, член-корреспондент ААН) Список сокращений:
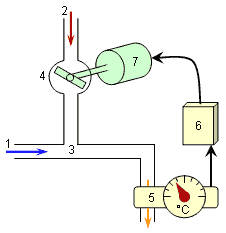
1. Общие соображения В истории науки математические приемы неоднократно рождались при решении прикладных задач. Но, перед тем, как стать достоянием других областей, они становились разделами собственно математики. Метод должен “войти в моду”, быть признан и оценен, включен в учебники и программы, причем на той стадии образования и с той степенью массовости, которые соответствовали бы его научным и дидактическим свойствам (доступность, поучительность, спектр возможных приложений, эффективность использования). Здесь речь о методе, с которым этого не произошло, несмотря на успешную и длительную апробацию в одной из областей. Он давно стал в ней типовым приемом. Но распространение на другие сферы идет крайне медленно, попытки – разрозненны и не подкрепляются базовым образованием. Метод неизвестен большинству из тех, кому он необходим для практической работы (инженеры, врачи, биологи всех направлений, экологи, экономисты – за редкими исключениями), и тем, кто должен бы их к этому готовить (школьные и вузовские учителя математики, физики, прикладных наук). Как когда-то умение делить большие числа считалось великим искусством. Метод структурных схем (МСС) был создан для нужд теории автоматического управления (ТАУ) и стал в ней типовым приемом для описания, исследования и расчетов сложных систем контроля, регулирования, управления (САК, САР, САУ). Здесь рассматривается лишь небольшая часть его возможностей, обусловленных простейшими сторонами метода, которые поддаются адаптации к школьному и минимальному из вузовских курсов математики и общему уровню математической подготовки в массовых профессиях. Ниже следует именно такое, сильно урезанное описание метода. Простейшая задача регулирования – поддержание на заданном уровне какого-либо технологического параметра (температуры воды в отопительной системе, высоты полета самолета на курсе, и т.д.). Для этого требуется в очень простой форме учесть зависимость между управляющим фактором и регулируемой величиной. Допустим, что температуру воды регулируют смешением холодной и горячей воды; температуры той и другой и расход холодной воды постоянны (см. рис.1). Система состоит из трубопроводов холодной (1) и горячей (2) воды, смесителя (3), заслонки (4) на трубе горячей воды, измерителя температуры (5), регулятора (6) с задатчиком температуры и усилителем, и исполнительного механизма (7). Температуру воды непрерывно измеряют, ее значение сравнивают с заданным. При наличии разницы между ними регулятор вырабатывает команду на поворот заслонки, меняющей расход горячей воды, до тех пор, пока эта разница не исчезнет. Независимая переменная (входной фактор, или вход системы) – заданное значение температуры. Выходные функции (выходы) – угол поворота заслонки, расход горячей добавки, температура смеси. Нас интересует зависимость между входом и каждым из выходов.
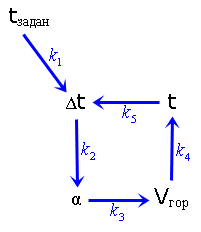
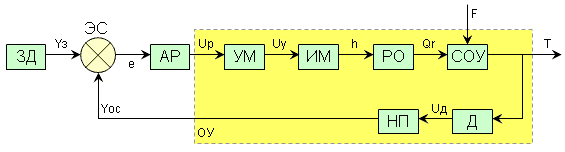
На самом деле, главная задача, решаемая ТАУ – качество регулирования – требует учета динамических свойств объекта. Ее мы рассматривать не будем, и ограничимся только статикой. Уже в этом простом примере возникают проблемы. Зависимость расхода горячей добавки от угла поворота заслонки плохо описывается теоретически и скорее всего нелинейна. Зависимость конечной температуры от этого расхода описать несложно, но существуют трудно учитываемые тепловые потери и погрешности измерения расходов и температур. В реальных задачах добавляется проблема обозримости, связанная с большим числом параметров. Например, в системе управления электростанцией оно достигает десятков (значения расходов, давлений, температур, чисел оборотов, напряжений, токов, передаваемых мощностей в разных участках сети, и т.д.). Создатели МСС поступили очень просто и экономно. Для обеспечения обозримости системы, связи между ее параметрами изображают не уравнениями, а структурной схемой (на рисунке справа). Стрелки на схеме соответствуют влияниям: 1, 5 – заданной и фактической температур на их разность, 2 – этой разности на угол поворота заслонки (управление), 3 – угла поворота на расход горячей добавки, 4 – этой добавки на температуру смеси. Стрелки 2, 3, 4, 5 образуют отрицательную обратную связь. Ее знак обеспечивается надлежащим подбором характеристик связей 2, 3. Возможны разные формы представления схем. Здесь принята форма ориентированного графа: обозначения параметров связаны стрелками. Для расширительного толкования МСС она удобнее обычно применяемой в ТАУ формы. Для простоты количественных оценок зависимости линеаризуют. Каждое звено характеризуется коэффициентом передачи – производной его выхода по входу в разомкнутом состоянии, то есть, без учета влияния остальных звеньев. Получаем зависимости вида: Отклонения отсчитываются от базы, или номинального, заданного режима. Задача сводится к определению результирующего коэффициента передачи системы (РКП) по ее структуре и коэффициентам передачи звеньев. Она решается путем эквивалентных преобразований схемы, в ходе которых последняя свертывается и сводится, в конечном счете, к единственному звену. Правила преобразований вытекают из правил дифференцирования и решения систем линейных алгебраических уравнений. Основных правил три: • при объединении последовательных звеньев их коэффициенты передачи перемножаются; • при объединении параллельных звеньев их коэффициенты передачи складываются; • при объединении антипараллельных звеньев они образуют замкнутую петлю при одном из узлов, при удалении которой коэффициенты передачи всех стрелок, приходящих в этот узел, делятся на знаменатель вида: единица минус коэффициент передачи указанной петли. Владение техникой метода сводится к умению выполнять такие преобразования для схем разной структуры. Например, для приведенной схемы выражение для РКП по каналу ( Для канала ( Замечание 1. В статике это условие недостижимо: оно требует бесконечно большого коэффициента усиления ОС, и реально имеет место статическая ошибка регулирования. Но мы договорились оставить динамику в стороне. Замечание 2. В знаменателе этой формулы в руководствах по ТАУ обычно указывают знак ±, имея в виду, что при проектировании систем выбирается нужный вариант знака. Но, при использовании для других целей, удобнее однозначная формула, с определением знака по знакам всех КП. В любой прикладной области приходится решать задачи, где связи между параметрами в сложном объекте описываются системой уравнений (вообще говоря, нелинейных). Далеко не всегда их стоит решать “в лоб” по следующим причинам. 1) Такая система не всегда разрешима аналитически, а если разрешима, то решение бывает чрезмерно громоздким. 2) Значения аргументов и констант нередко известны с малой точностью, что делает бессмысленной погоню за кажущейся строгостью. 3) Реально в таких задачах обычно требуется определить не столько значения искомых функций, сколько влияние на них входов системы. Естественная мера искомого влияния – производная выхода по входу; ее-то определение и должно быть нашей главной целью. Следовательно, задача в математической формулировке сводится к дифференцированию сложной неявно заданной функции. Ее производную нужно выразить через значения аргументов, а возможно – и функций. Эти значения для всех выходных и промежуточных величин в исходной (базовой) точке считаются известными. Для ближней окрестности базовой точки получаем линейную модель. При больших отклонениях от базы, когда точность такой модели становится недостаточной, выражение для производной можно считать дифференциальным уравнением и интегрировать его от базовых значений, как начальных условий (этот случай оставим в стороне, ограничившись упоминанием о нем). Составная часть операции ДСНФ – решение системы уравнений, связывающих между собой частные производные между параметрами исходной системы. Принципиальная особенность этой системы – ее линейность, независимо от характера связей в исходной системе. Бросается в глаза изоморфность этой задачи рассмотренной выше задаче ТАУ, и напрашивается вывод о возможности использования МСС для чисто математических приложений. Дифференцирование сложного выражения с помощью МСС начинается с составления его структурной схемы. Выражение как бы разбирается на составные части, а схема показывает, как они между собой связаны. Этот этап – главный по затрате умственных усилий во всей процедуре. Остающиеся два этапа можно выполнять независимо один от другого в любой последовательности: определение КП частных связей (это и есть собственно дифференцирование), и свертывание схемы по известным правилам с определением РКП. Тем самым задача решена – РКП и есть искомая производная. Сводить ее в единую формулу, подставляя все промежуточные выражения, не обязательно, а иногда и нежелательно. Стремиться к этому имеет смысл, лишь когда ее затем можно дополнительно упростить. При очень густой сети взаимных связей, когда преобразования становятся чрезмерно громоздкими, их можно заменить решением уравнений в стандартной матричной форме (прибегать к этому приходится сравнительно редко). Итак, МСС по своей сути есть рациональный прием дифференцирования сложных, и особенно – неявно заданных функций, и его с успехом можно применять для собственных нужд математики. Но о нем не упоминают ни в вузовских, ни, тем более, в школьных учебниках математики. Тому есть два объяснения. Первое. Метод появился много позже того, как правила дифференцирования сложились, были отшлифованы поколениями учебников и стали казаться чем–то незыблемым. Сам же он излагается в прикладных курсах, и большинству математиков просто неизвестен. Как сказал Н.Н.Моисеев, “стиль наших математиков – не замечать сделанного не ими” [3]. Второе. Указанное изложение жестко привязано к нуждам конкретной области, вводится на более сложной математической базе, чем требуется в большинстве приложений, игнорирует требования дидактики и засорено местными жаргонизмами. Поясним это на конкретном примере. На рис.2 изображена структурная схема системы регулирования в том виде, как это принято в большинстве руководств по ТАУ. Пример взят из публикации в Интернете [1] и подвергнут незначительной редакционной правке.
Согласно принятой терминологии, система состоит из звеньев. На схеме их изображают прямоугольниками, соединенными стрелками. Обратим внимание: все звенья соответствуют конкретным материальным объектам, перечисленным в списке условных обозначений. А поскольку схема помещена в учебной статье, как образец для подражания, то у начинающего неизбежно складывается впечатление, что иначе и быть не может. Это замечание – не к данной конкретной публикации, а к стилю изложения, общепринятому в ТАУ, за редчайшими исключениями. Например, в [2] показан переход к схеме в виде ориентированного графа (названного сигнальным графом), но, даже и там, в качестве основного, принят обычный вариант схемы. Хотя оба способа изображения схем эквивалентны, в дидактическом смысле они неравноценны, что можно видеть, сравнивая рис. 1 и 2. Параметры на «обычной» схеме совершенно теряются. На графе (рис.1) они четко видны, будучи изображены узлами графа, и ясна система взаимных связей между ними, показанных стрелками. Стрелки – это и есть звенья, но они совершенно не обязательно являются материальными объектами. Так, стрелка Звенья обладают статическими и динамическими характеристиками. Динамические характеристики задаются передаточными функциями, статические – коэффициентами передачи. Правила преобразований для них одинаковы, и в ТАУ их обычно вводят сразу для общего случая. Но понятие передаточной функции основано на специальном математическом аппарате – операционном исчислении, требующем, в свою очередь, знания ТФКП. Ничего этого не требуется для статического случая, где нужно владеть лишь понятием производной. Догадаться о возможности расширить сферу приложения метода при таких обстоятельствах весьма затруднительно. Итак, недоступность аппарата МСС широкому кругу потенциальных пользователей – результат встречного проявления двух разновидностей профессионального снобизма: один со стороны математиков, другой – со стороны его описаний в ТАУ. Для преодоления того и другого, были предназначены учебные пособия [4],[5],[6a][6b],[7]. Процедура ДСНФ состоит из двух совершенно различных операций – собственно дифференцирования и сопутствующих преобразований. Выполнение их вперемешку раздваивает внимание и провоцирует ошибки. Иными словами, в традиционном ее исполнении нарушен основной принцип научной организации труда (НОТ), требующий объединять однородные и разделять разнородные операции. МСС осуществляет такую сепарацию и группировку, обеспечивая выполнение правил НОТ. На что расходуются главные усилия при преобразовании сложных формул? Если действовать последовательно, не пропуская ни одного этапа и фиксируя промежуточные результаты, приходится многократно переписывать одни и те же громоздкие выражения. Каждое такое переписывание – повод потерять сомножитель, слагаемое или знак. Противоположный стиль – сразу записывать готовый ответ, выполняя промежуточные действия “в уме” – требует высочайшей сосредоточенности, и при малейшем отвлечении внимания или утомлении ошибки неизбежны, а главное – трудно обнаружимы. Структурная схема облегчает оба пути. С ее помощью легче сразу увидеть готовый результат, а при “многоступенчатой” работе – сводить переписывание лишь к самому необходимому; поиск ошибок существенно облегчается. Понятно, что опытному математику в сравнительно простых задачах МСС ничего нового не дает, и он с успехом обходится без него. Но, во-первых, для начинающих это совсем не так. Во-вторых, не все задачи столь уж просты и для искушенного исполнителя. Если в исходную формулу входят не 3-10, а, например, тридцать-сорок фрагментов, то и ему лучше не бравировать своими способностями, а воспользоваться схемой. В действительности приложения к математике не ограничиваются одним ее разделом: дифференцирование входит составной частью в ряд других операций (интегрирование, решение систем дифференциальных уравнений, вероятностные расчеты и др.). Но при всей полезности чисто математических приложений, не это само по себе побудило привлечь к ним внимание. Гораздо важнее перебросить мостик от теоретических первооснов к будущим реальным приложениям. Ведь одни и те же идеи воспринимаются совершенно по-разному в зависимости от окружения, в котором они преподносятся. МСС, изучаемый на 3-м курсе института в составе курса автоматики – это всего лишь еще один специальный прикладной вопрос, относящийся только к этой профессии. У студентов других профессий, изучающих ту же автоматику как не основной (а значит – второстепенный, “не нужный”) предмет, он удерживается в памяти в лучшем случае до экзамена или зачета. Но тот же МСС, буде изучен в курсе математики, увязан с ее идеями и обкатан на ее собственных задачах – это уже часть базового образования, формирующая мировоззрение, образ мышления, даже интуицию. В том же курсе автоматики, с ним столкнется не спотыкающийся на каждом шагу новичок, а уверенно владеющий им специалист. И сам метод для него – уже не объект изучения, а рабочий инструмент. К тому же, поскольку правила преобразований, изученные для статики, полностью сохраняются при переходе к динамическим задачам, предварительное изучение МСС на адаптированном уровне – удобная промежуточная ступень для перехода к полному варианту. Сказанное относится к традиционной сфере приложений МСС. Но его адаптация создает предпосылки для расширения этой сферы, и сейчас даже нельзя перечислить все потенциально новые области. Надо ли говорить, как это скажется на общем уровне образованности? И при этом – с экономией времени и усилий! |
|||||||
, где x, y – вход и выход звена (или схемы в целом); k – коэффициент, имеющий несколько названий: коэффициент усиления, коэффициент передачи (дальше будем пользоваться этим названием), коэффициент чувствительности, а по сути – производная выхода по входу.
) примет вид: 
) его нужно еще домножить на 
. При оптимальном управлении этот РКП должен быть равен единице – в этом и состоит смысл управления.